About

These blogs are my notes that represent my interpretation of the CS236 course taught by Stefano.

Continuing..

A variational approximation to the posterior

For cases when p(z|x; θ) is intractable we come up with a tractable approximation q(z; ϕ) that is as close as possible to p(z|x; θ)

In the case of an image having it’s top half unknown this is what we came up with the last time

• We assumed p(z, x; θ) is close to pdata (z, x). z denotes the top half of the image (assumed to be latent)
• And theorized q(xtop ; ϕ) a (tractable) probability distribution over the hidden variables (missing pixels in this example) xtop parameterized by ϕ (variational parameters)

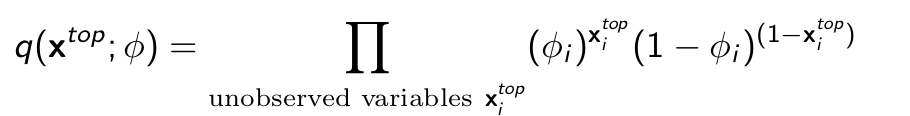
Given the probablity distribution we deduced that the last choice is probably the best one

• Is ϕi = 0.5 ∀i a good approximation to the posterior p(xtop |xbottom ; θ)? No
• Is ϕi = 1 ∀i a good approximation to the posterior p(xtop |xbottom ; θ)? No
• Is ϕi ≈ 1 for pixels i corresponding to the top part of digit 9 a good approximation? Yes

Learning via stochastic variational inference (SVI)

Our goal is to optimize ELBO given below.

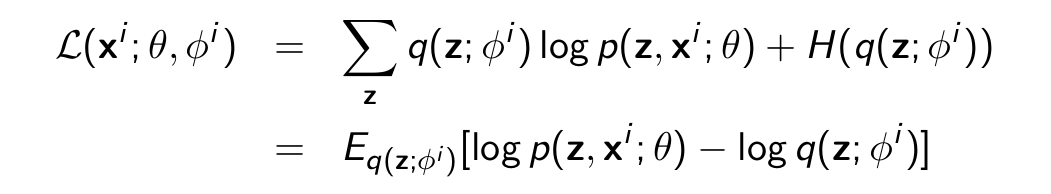
Steps:

• Initialize θ, ϕ1 , · · · , ϕM
• Randomly sample a data point xi from D
• Optimize L(xi ; θ, ϕi ) as a function of ϕi :
  • Repeat ϕi = ϕi + η∇ϕi L(xi ; θ, ϕi )
  • until convergence to ϕi,∗ ≈ arg maxϕ L(xi ; θ, ϕ)
• Compute ∇θ L(xi ; θ, ϕi,∗ )
• Update θ in the gradient direction. Go to step 2

How to compute the gradients? There might not be a closed form solution for the expectations. So we use Monte Carlo sampling

To evaluate the bound, sample z1 , · · · , zK from q(z; ϕ) and estimate

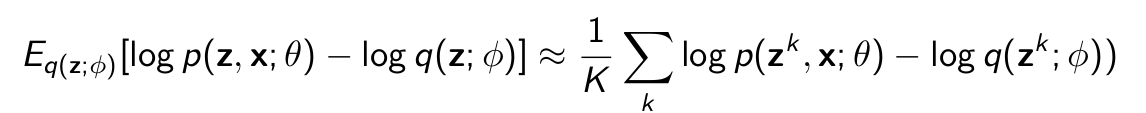
Calculate gradients w.r.t θ and ϕ on the Monte-Carlo estimate.

Key assumption: q(z; ϕ) is tractable, i.e., easy to sample from and evaluate

The gradient with respect to θ is easy

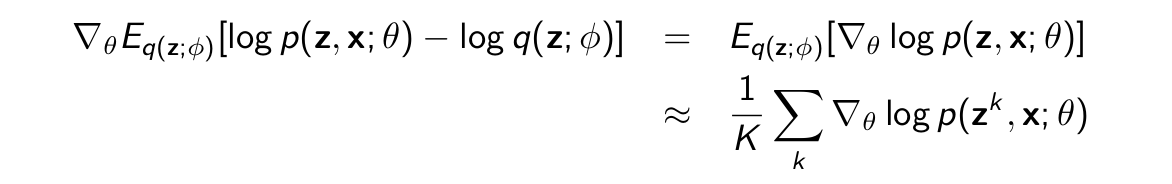
The gradient with respect to ϕ is more complicated because the expectation depends on ϕ

We still want to estimate with a Monte Carlo average

Reparametrization

Want to compute a gradient with respect to ϕ of

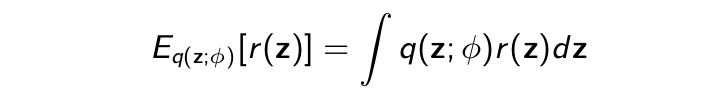
where z is now continuous

Suppose q(z; ϕ) = N (µ, σ 2 I ) is Gaussian with parameters ϕ = (µ, σ). These are equivalent ways of sampling

• Sample z ∼ q(z; ϕ)
• Sample ϵ ∼ N (0, I ), z = µ + σϵ = g (ϵ; ϕ). g is deterministic!

Using this equivalence we compute the expectation in two ways:

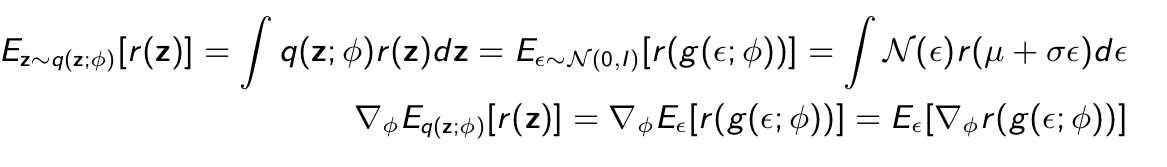
Easy to estimate via Monte Carlo if r and g are differentiable w.r.t. ϕ and ϵ is easy to sample from (backpropagation)

Using Reparametrization for ELBO

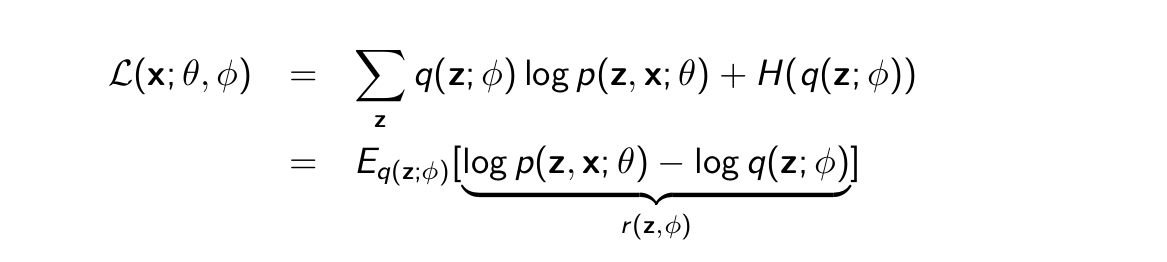Using the reparameterization trick in ELBO. We can rewrite our equation as Eq(z;ϕ) [r (z, ϕ)] but if we observe it is not the same as Eq(z;ϕ) [r (z)] as our inner value in expectation depends on ϕ

Does this change this? Yes Can we still use reparametrization? Yes

Assume z = µ + σϵ = g (ϵ; ϕ) like before. Then

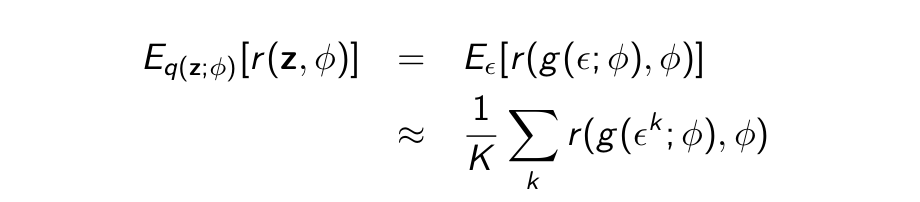
Amortized Inference

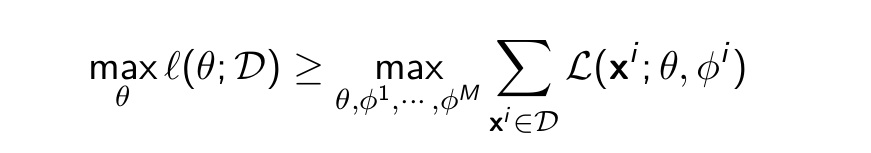
• So far we have used a set of variational parameters ϕi for each data point xi . Does not scale to large datasets.
• Amortization: Now we learn a single parametric function fλ that maps each x to a set of (good) variational parameters. Like doing regression on xi → ϕi,∗
  • For example, if q(z|xi ) are Gaussians with different means µ1 , · · · , µm , we learn a single neural network fλ mapping xi to µi
• We approximate the posteriors q(z|xi ) using this distribution qλ (z|x)

Once again…

• Assume p(z, xi ; θ) is close to pdata (z, xi ). Suppose z captures information such as the digit identity (label), style, etc.
• q(z; ϕi ) is a (tractable) probability distribution over the hidden variables z parameterized by ϕi (variational parameters)
• For each xi , need to find a good ϕi,∗ (via optimization, expensive).
• Amortized inference: learn how to map xi to a good set of parameters ϕi via q(z; fλ (xi )). fλ learns how to solve the optimization problem for you
• For simplicity we refer q(z; fλ (xi)) as qϕ (z|x)

Learning with Amortized Inference

As before, optimize ELBO as a function of θ, ϕ using (stochastic) gradient descent

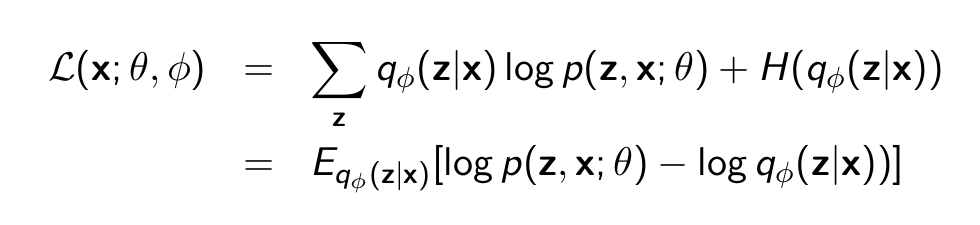
• Initialize θ(0) , ϕ(0)
• Randomly sample a data point xi from D
• Compute ∇θ L(xi ; θ, ϕ) and ∇ϕ L(xi ; θ, ϕ)
• Update θ, ϕ in the gradient direction
• How to compute the gradients? Use reparameterization like before

Autoencoder: Perspective

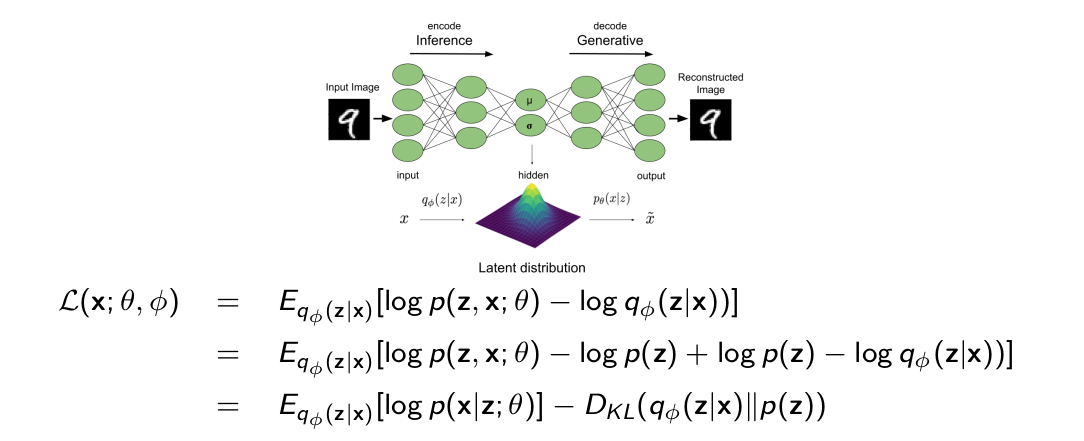
• Take a data point xi , map it to ẑ by sampling from qϕ (z|xi ) (encoder). Sample from a Gaussian with parameters (µ, σ) = encoderϕ (xi )
• Reconstruct x̂ by sampling from p(x|ẑ; θ) (decoder). Sample from a Gaussian with parameters decoderθ (ẑ)

What does the training objective L(x; θ, ϕ) do?

• First term encourages x̂ ≈ xi (xi likely under p(x|ẑ; θ)). Autoencoding loss!
• Second term encourages ẑ to have a distribution similar to the prior p(z)\

Intution behind the two terms?

• The first part is supposed to help us give likely completions given z. Or in terms of the perspective of the decoder it means that given x̂ from encoder we should be able to reconstruct xi
• Second term encourages ẑ to have a distribution similar to the prior p(z)

Continued

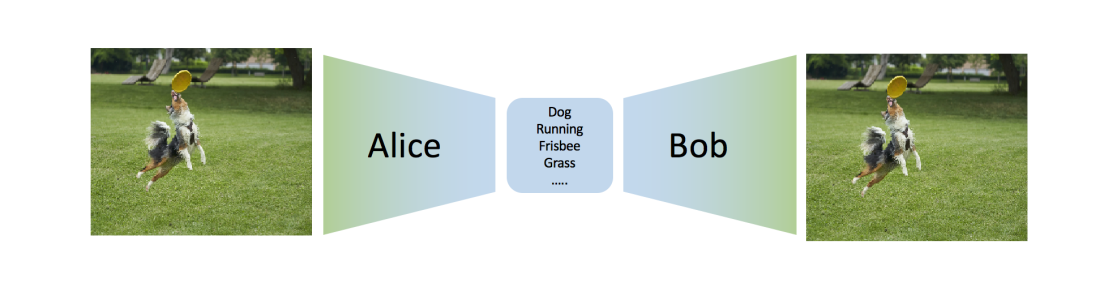
• Alice goes on a space mission and needs to send images to Bob. Given an image xi , she (stochastically) compresses it using ẑ ∼ qϕ (z|xi ) obtaining a message ẑ. Alice sends the message ẑ to Bob

• Given ẑ, Bob tries to reconstruct the image using p(x|ẑ; θ)

  • This scheme works well if Eqϕ (z|x) [log p(x|z; θ)] is large
  • The term DKL (qϕ (z|x)∥p(z)) forces the distribution over messages to have a specific shape p(z). If Bob knows p(z), he can generate realistic messages ẑ ∼ p(z) and the corresponding image, as if he had received them from Alice!

Summary of Latent Variable Models

• Combine simple models to get a more flexible one (e.g., mixture of Gaussians)
• Directed model permits ancestral sampling (efficient generation): z ∼ p(z), x ∼ p(x|z; θ)
• However, log-likelihood is generally intractable, hence learning is difficult
• Joint learning of a model (θ) and an amortized inference component (ϕ) to achieve tractability via ELBO optimization
• Latent representations for any x can be inferred via qϕ (z|x)